Fibonacci in Knitting and Designs
You've probably heard this word somewhere but couldn't tell if it means a new kind of fiber, a special sort of pasta, a secret described in the DaVinci Code or a town in Italy......
The Fibonacci sequence was introduced by a medieval mathematician Leonardo of Pisa, also known as Fibonacci."In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:
The Fibonacci sequence was introduced by a medieval mathematician Leonardo of Pisa, also known as Fibonacci."In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:
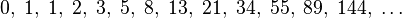 .
.
By definition, the first two Fibonacci numbers are 0 and 1, and each subsequent number is the sum of the previous two. Some sources omit the initial 0, instead beginning the sequence with two 1s." (Wikipedia)
The Fibonacci sequences are not only found in nature but are frequently used in music, art, design and architecture. Since these numbers create a very eye pleasing patterning or structure I love to incorporate them in knit wear design.
Following Wallaby Sweater I made for charity is an example of it. The teenager asked for grass green and white in a hooded sweater. To make the striping more interesting for the eye I used Fibonacci numbers:
The Fibonacci sequences are not only found in nature but are frequently used in music, art, design and architecture. Since these numbers create a very eye pleasing patterning or structure I love to incorporate them in knit wear design.
Following Wallaby Sweater I made for charity is an example of it. The teenager asked for grass green and white in a hooded sweater. To make the striping more interesting for the eye I used Fibonacci numbers:
In this case I used them for two colors going in the same direction for the stockinette part after finishing the bottom ribbing.
21 rows green - 21 rows white
13 rows green - 13 rows white
8 rows green - 8 rows white
5 rows green - 5 rows white
3 rows green - 3 rows white
2 rows green - 2 rows white
1 row green - 1 row white
It also can be done in opposite directions for the colors. Here an example how it would work in the wallaby sweater
g (green) - w (white)
21 rows g - 1 row w
13 rows g - 2 rows w
8 rows g - 3 rows w
5 rows g - 5 rows w
3 rows g - 8 rows w
2 rows g - 13 rows w
1 row g - 21 rows w
You can also use more than two colors to create an interesting striping effect which is not boring and helps you to use up odds and ends. It also works great in socks, mittens, hats, scarfs, felted bags; basically all knitting projects you can think of.
You can even create cool pattern effects with Fibonacci sequences for borders or accents like this exaple:
These are some simple ways to play with these numbers and there are endless possibilities to use them for your design or knitting project........
21 rows green - 21 rows white
13 rows green - 13 rows white
8 rows green - 8 rows white
5 rows green - 5 rows white
3 rows green - 3 rows white
2 rows green - 2 rows white
1 row green - 1 row white
It also can be done in opposite directions for the colors. Here an example how it would work in the wallaby sweater
g (green) - w (white)
21 rows g - 1 row w
13 rows g - 2 rows w
8 rows g - 3 rows w
5 rows g - 5 rows w
3 rows g - 8 rows w
2 rows g - 13 rows w
1 row g - 21 rows w
You can also use more than two colors to create an interesting striping effect which is not boring and helps you to use up odds and ends. It also works great in socks, mittens, hats, scarfs, felted bags; basically all knitting projects you can think of.
You can even create cool pattern effects with Fibonacci sequences for borders or accents like this exaple:
These are some simple ways to play with these numbers and there are endless possibilities to use them for your design or knitting project........







Comments